Mixing
integral kernel function for the SU(N) group
Clash Royale CLAN TAG#URR8PPP
up vote
3
down vote
favorite
It is well know that the Haar probability measure for the $U(N)$ group, given by
$$
beginalign
dX_U(N) & = frac1N!(2pi)^N
beginvmatrix
1 & 1 & cdots & 1 & 1 \
e^ilambda_1 & e^ilambda_2 & cdots & e^ilambda_N-1 & e^ilambda_N \
e^i2lambda_1 & e^i2lambda_2 & cdots & e^i2lambda_N-1 & e^i2lambda_N \
vdots & vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & e^i(N-1)lambda_2 & cdots & e^i(N-1)lambda_N-1 & e^i(N-1)lambda_N \
endvmatrix^2 dlambda_1dots dlambda_N \
& = frac1N!(2pi)^N prod_1leq j<kleq N |e^ilambda_j-e^ilambda_k|^2 dlambda_1dots dlambda_N
endalign
$$
can also be expressed as a determinantal point process
$$ dX_U(N) = frac1N!(2pi)^N det_NXN(S_N(lambda_j,lambda_k))_1leq j,kleq N text dlambda_1dots dlambda_N $$
where
$$S_N(x,y)=fracsinfracN(x-y)2sinfracx-y2$$
is the integral kernel function for the $U(N)$ group (a proof of this fact can be found, for example, in section 4.1 of this paper); similar kernels have also been found for the special orthogonal and symplectic groups.
My question is whether any analogous kernel function is know for the $SU(N)$ group ? (or if it can be proved that it doesn't exist).
If such a function $K(x,y)$ exists, it would allow one to express the $SU(N)$ Haar probability measure
$$
beginalign
dX_SU(N) & = frac1N!(2pi)^N-1
beginvmatrix
1 & cdots & 1 & 1 \
e^ilambda_1 & cdots & e^ilambda_N-1 & e^-i(lambda_1+ldots+lambda_N-1) \
e^i2lambda_1 & cdots & e^i2lambda_N-1 & e^-i2(lambda_1+ldots+lambda_N-1) \
vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & cdots & e^i(N-1)lambda_N-1 & e^-i(N-1)(lambda_1+ldots+lambda_N-1) \
endvmatrix^2 dlambda_1dots dlambda_N-1 \
& = frac1N!(2pi)^N-1 prod_1leq j<kleq N-1 |e^ilambda_j-e^ilambda_k|^2 prod_1leq jleq N-1 |e^ilambda_j-e^-i(lambda_1+ldots+lambda_N-1)|^2 dlambda_1dots dlambda_N-1 \
endalign
$$
in the form of
$$ dX_SU(N) = frac1N!(2pi)^N-1 det_(N-1)X(N-1)(K(lambda_j,lambda_k))_1leq j,kleq N-1 text dlambda_1dots dlambda_N-1 $$
fa.functional-analysis random-matrices determinants integral-kernel
asked 4 hours ago
Amadocta
664
add a comment |Â
up vote
3
down vote
favorite
It is well know that the Haar probability measure for the $U(N)$ group, given by
$$
beginalign
dX_U(N) & = frac1N!(2pi)^N
beginvmatrix
1 & 1 & cdots & 1 & 1 \
e^ilambda_1 & e^ilambda_2 & cdots & e^ilambda_N-1 & e^ilambda_N \
e^i2lambda_1 & e^i2lambda_2 & cdots & e^i2lambda_N-1 & e^i2lambda_N \
vdots & vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & e^i(N-1)lambda_2 & cdots & e^i(N-1)lambda_N-1 & e^i(N-1)lambda_N \
endvmatrix^2 dlambda_1dots dlambda_N \
& = frac1N!(2pi)^N prod_1leq j<kleq N |e^ilambda_j-e^ilambda_k|^2 dlambda_1dots dlambda_N
endalign
$$
can also be expressed as a determinantal point process
$$ dX_U(N) = frac1N!(2pi)^N det_NXN(S_N(lambda_j,lambda_k))_1leq j,kleq N text dlambda_1dots dlambda_N $$
where
$$S_N(x,y)=fracsinfracN(x-y)2sinfracx-y2$$
is the integral kernel function for the $U(N)$ group (a proof of this fact can be found, for example, in section 4.1 of this paper); similar kernels have also been found for the special orthogonal and symplectic groups.
My question is whether any analogous kernel function is know for the $SU(N)$ group ? (or if it can be proved that it doesn't exist).
If such a function $K(x,y)$ exists, it would allow one to express the $SU(N)$ Haar probability measure
$$
beginalign
dX_SU(N) & = frac1N!(2pi)^N-1
beginvmatrix
1 & cdots & 1 & 1 \
e^ilambda_1 & cdots & e^ilambda_N-1 & e^-i(lambda_1+ldots+lambda_N-1) \
e^i2lambda_1 & cdots & e^i2lambda_N-1 & e^-i2(lambda_1+ldots+lambda_N-1) \
vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & cdots & e^i(N-1)lambda_N-1 & e^-i(N-1)(lambda_1+ldots+lambda_N-1) \
endvmatrix^2 dlambda_1dots dlambda_N-1 \
& = frac1N!(2pi)^N-1 prod_1leq j<kleq N-1 |e^ilambda_j-e^ilambda_k|^2 prod_1leq jleq N-1 |e^ilambda_j-e^-i(lambda_1+ldots+lambda_N-1)|^2 dlambda_1dots dlambda_N-1 \
endalign
$$
in the form of
$$ dX_SU(N) = frac1N!(2pi)^N-1 det_(N-1)X(N-1)(K(lambda_j,lambda_k))_1leq j,kleq N-1 text dlambda_1dots dlambda_N-1 $$
fa.functional-analysis random-matrices determinants integral-kernel
asked 4 hours ago
Amadocta
664
add a comment |Â
up vote
3
down vote
favorite
up vote
3
down vote
favorite
It is well know that the Haar probability measure for the $U(N)$ group, given by
$$
beginalign
dX_U(N) & = frac1N!(2pi)^N
beginvmatrix
1 & 1 & cdots & 1 & 1 \
e^ilambda_1 & e^ilambda_2 & cdots & e^ilambda_N-1 & e^ilambda_N \
e^i2lambda_1 & e^i2lambda_2 & cdots & e^i2lambda_N-1 & e^i2lambda_N \
vdots & vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & e^i(N-1)lambda_2 & cdots & e^i(N-1)lambda_N-1 & e^i(N-1)lambda_N \
endvmatrix^2 dlambda_1dots dlambda_N \
& = frac1N!(2pi)^N prod_1leq j<kleq N |e^ilambda_j-e^ilambda_k|^2 dlambda_1dots dlambda_N
endalign
$$
can also be expressed as a determinantal point process
$$ dX_U(N) = frac1N!(2pi)^N det_NXN(S_N(lambda_j,lambda_k))_1leq j,kleq N text dlambda_1dots dlambda_N $$
where
$$S_N(x,y)=fracsinfracN(x-y)2sinfracx-y2$$
is the integral kernel function for the $U(N)$ group (a proof of this fact can be found, for example, in section 4.1 of this paper); similar kernels have also been found for the special orthogonal and symplectic groups.
My question is whether any analogous kernel function is know for the $SU(N)$ group ? (or if it can be proved that it doesn't exist).
If such a function $K(x,y)$ exists, it would allow one to express the $SU(N)$ Haar probability measure
$$
beginalign
dX_SU(N) & = frac1N!(2pi)^N-1
beginvmatrix
1 & cdots & 1 & 1 \
e^ilambda_1 & cdots & e^ilambda_N-1 & e^-i(lambda_1+ldots+lambda_N-1) \
e^i2lambda_1 & cdots & e^i2lambda_N-1 & e^-i2(lambda_1+ldots+lambda_N-1) \
vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & cdots & e^i(N-1)lambda_N-1 & e^-i(N-1)(lambda_1+ldots+lambda_N-1) \
endvmatrix^2 dlambda_1dots dlambda_N-1 \
& = frac1N!(2pi)^N-1 prod_1leq j<kleq N-1 |e^ilambda_j-e^ilambda_k|^2 prod_1leq jleq N-1 |e^ilambda_j-e^-i(lambda_1+ldots+lambda_N-1)|^2 dlambda_1dots dlambda_N-1 \
endalign
$$
in the form of
$$ dX_SU(N) = frac1N!(2pi)^N-1 det_(N-1)X(N-1)(K(lambda_j,lambda_k))_1leq j,kleq N-1 text dlambda_1dots dlambda_N-1 $$
fa.functional-analysis random-matrices determinants integral-kernel
asked 4 hours ago
Amadocta
664
It is well know that the Haar probability measure for the $U(N)$ group, given by
$$
beginalign
dX_U(N) & = frac1N!(2pi)^N
beginvmatrix
1 & 1 & cdots & 1 & 1 \
e^ilambda_1 & e^ilambda_2 & cdots & e^ilambda_N-1 & e^ilambda_N \
e^i2lambda_1 & e^i2lambda_2 & cdots & e^i2lambda_N-1 & e^i2lambda_N \
vdots & vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & e^i(N-1)lambda_2 & cdots & e^i(N-1)lambda_N-1 & e^i(N-1)lambda_N \
endvmatrix^2 dlambda_1dots dlambda_N \
& = frac1N!(2pi)^N prod_1leq j<kleq N |e^ilambda_j-e^ilambda_k|^2 dlambda_1dots dlambda_N
endalign
$$
can also be expressed as a determinantal point process
$$ dX_U(N) = frac1N!(2pi)^N det_NXN(S_N(lambda_j,lambda_k))_1leq j,kleq N text dlambda_1dots dlambda_N $$
where
$$S_N(x,y)=fracsinfracN(x-y)2sinfracx-y2$$
is the integral kernel function for the $U(N)$ group (a proof of this fact can be found, for example, in section 4.1 of this paper); similar kernels have also been found for the special orthogonal and symplectic groups.
My question is whether any analogous kernel function is know for the $SU(N)$ group ? (or if it can be proved that it doesn't exist).
If such a function $K(x,y)$ exists, it would allow one to express the $SU(N)$ Haar probability measure
$$
beginalign
dX_SU(N) & = frac1N!(2pi)^N-1
beginvmatrix
1 & cdots & 1 & 1 \
e^ilambda_1 & cdots & e^ilambda_N-1 & e^-i(lambda_1+ldots+lambda_N-1) \
e^i2lambda_1 & cdots & e^i2lambda_N-1 & e^-i2(lambda_1+ldots+lambda_N-1) \
vdots & ddots & vdots & vdots \
e^i(N-1)lambda_1 & cdots & e^i(N-1)lambda_N-1 & e^-i(N-1)(lambda_1+ldots+lambda_N-1) \
endvmatrix^2 dlambda_1dots dlambda_N-1 \
& = frac1N!(2pi)^N-1 prod_1leq j<kleq N-1 |e^ilambda_j-e^ilambda_k|^2 prod_1leq jleq N-1 |e^ilambda_j-e^-i(lambda_1+ldots+lambda_N-1)|^2 dlambda_1dots dlambda_N-1 \
endalign
$$
in the form of
$$ dX_SU(N) = frac1N!(2pi)^N-1 det_(N-1)X(N-1)(K(lambda_j,lambda_k))_1leq j,kleq N-1 text dlambda_1dots dlambda_N-1 $$
fa.functional-analysis random-matrices determinants integral-kernel
fa.functional-analysis random-matrices determinants integral-kernel
asked 4 hours ago
Amadocta
664
asked 4 hours ago
Amadocta
664
edited 2 hours ago
asked 4 hours ago
Amadocta
664
asked 4 hours ago
Amadocta
664
asked 4 hours ago
Amadocta
664
664
add a comment |Â
add a comment |Â
1 Answer
1
active
oldest
votes
up vote
3
down vote
The integral kernel for $rm U,(N)$, due to Dyson, has been generalized by Katz and Sarnak to other compact groups (Random Matrices, Frobenius Eigenvalues, and Monodromy, page 121). Their result has the general form
$$dmu=frac1n!det_ntimes n[L_N(lambda_i,lambda_j)]prod_i=1^nfracdlambda_isigmapi,;;lambda_iin[0,sigmapi],;;1leq ileq n,$$
$$S_N(x)=fracsin(Nx/2)sin(x/2),;;
L_N(x,y)=tfrac12sigma[S_rho N+tau(x-y)+varepsilon S_rho N+tau(x+y)].$$
The coefficients are tabulated as follows: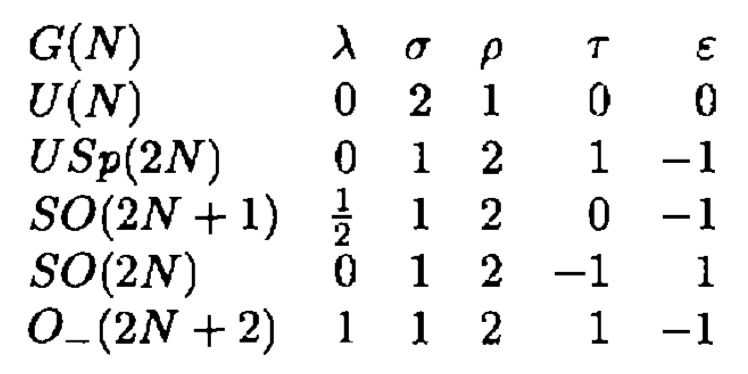
The group $rm SU,(N)$ is conspicuously missing from this table... I would assume there is a reason for this (Katz and Sarnak discuss $rm SU,(N)$ at various other points in their text). My surmise is that there is no way to incorporate the delta function $deltabigl(sum_i=1^N lambda_ibigr)$ into an $(N-1)times(N-1)$ determinant.
answered 1 hour ago
Carlo Beenakker
69k8155260
add a comment |Â
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
up vote
3
down vote
The integral kernel for $rm U,(N)$, due to Dyson, has been generalized by Katz and Sarnak to other compact groups (Random Matrices, Frobenius Eigenvalues, and Monodromy, page 121). Their result has the general form
$$dmu=frac1n!det_ntimes n[L_N(lambda_i,lambda_j)]prod_i=1^nfracdlambda_isigmapi,;;lambda_iin[0,sigmapi],;;1leq ileq n,$$
$$S_N(x)=fracsin(Nx/2)sin(x/2),;;
L_N(x,y)=tfrac12sigma[S_rho N+tau(x-y)+varepsilon S_rho N+tau(x+y)].$$
The coefficients are tabulated as follows: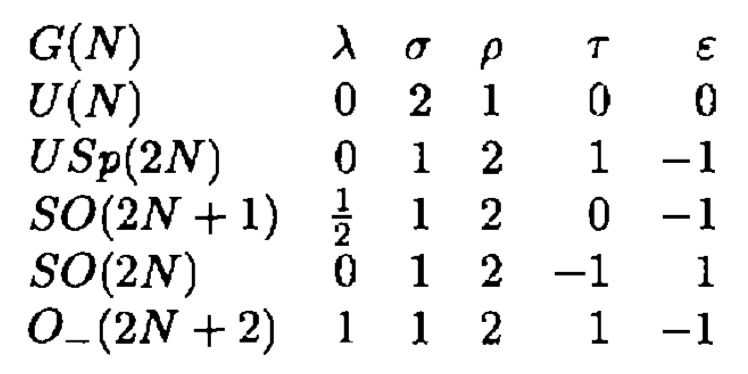
The group $rm SU,(N)$ is conspicuously missing from this table... I would assume there is a reason for this (Katz and Sarnak discuss $rm SU,(N)$ at various other points in their text). My surmise is that there is no way to incorporate the delta function $deltabigl(sum_i=1^N lambda_ibigr)$ into an $(N-1)times(N-1)$ determinant.
answered 1 hour ago
Carlo Beenakker
69k8155260
add a comment |Â
up vote
3
down vote
The integral kernel for $rm U,(N)$, due to Dyson, has been generalized by Katz and Sarnak to other compact groups (Random Matrices, Frobenius Eigenvalues, and Monodromy, page 121). Their result has the general form
$$dmu=frac1n!det_ntimes n[L_N(lambda_i,lambda_j)]prod_i=1^nfracdlambda_isigmapi,;;lambda_iin[0,sigmapi],;;1leq ileq n,$$
$$S_N(x)=fracsin(Nx/2)sin(x/2),;;
L_N(x,y)=tfrac12sigma[S_rho N+tau(x-y)+varepsilon S_rho N+tau(x+y)].$$
The coefficients are tabulated as follows: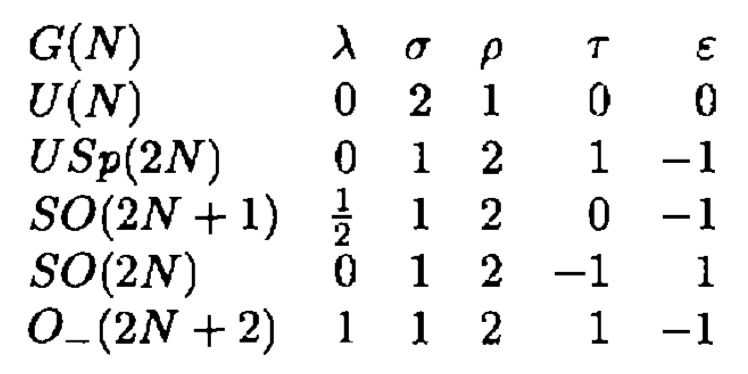
The group $rm SU,(N)$ is conspicuously missing from this table... I would assume there is a reason for this (Katz and Sarnak discuss $rm SU,(N)$ at various other points in their text). My surmise is that there is no way to incorporate the delta function $deltabigl(sum_i=1^N lambda_ibigr)$ into an $(N-1)times(N-1)$ determinant.
answered 1 hour ago
Carlo Beenakker
69k8155260
add a comment |Â
up vote
3
down vote
up vote
3
down vote
The integral kernel for $rm U,(N)$, due to Dyson, has been generalized by Katz and Sarnak to other compact groups (Random Matrices, Frobenius Eigenvalues, and Monodromy, page 121). Their result has the general form
$$dmu=frac1n!det_ntimes n[L_N(lambda_i,lambda_j)]prod_i=1^nfracdlambda_isigmapi,;;lambda_iin[0,sigmapi],;;1leq ileq n,$$
$$S_N(x)=fracsin(Nx/2)sin(x/2),;;
L_N(x,y)=tfrac12sigma[S_rho N+tau(x-y)+varepsilon S_rho N+tau(x+y)].$$
The coefficients are tabulated as follows: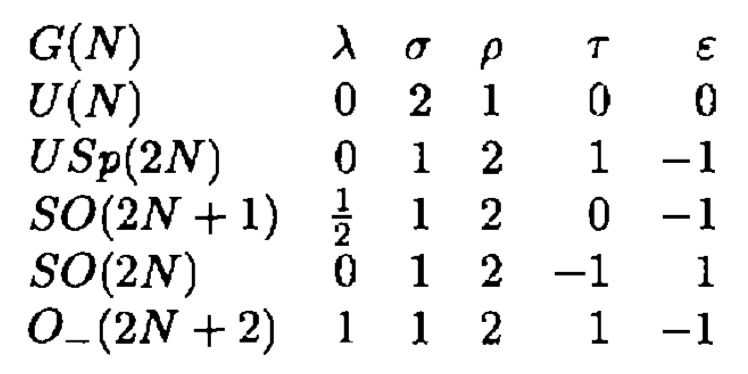
The group $rm SU,(N)$ is conspicuously missing from this table... I would assume there is a reason for this (Katz and Sarnak discuss $rm SU,(N)$ at various other points in their text). My surmise is that there is no way to incorporate the delta function $deltabigl(sum_i=1^N lambda_ibigr)$ into an $(N-1)times(N-1)$ determinant.
answered 1 hour ago
Carlo Beenakker
69k8155260
The integral kernel for $rm U,(N)$, due to Dyson, has been generalized by Katz and Sarnak to other compact groups (Random Matrices, Frobenius Eigenvalues, and Monodromy, page 121). Their result has the general form
$$dmu=frac1n!det_ntimes n[L_N(lambda_i,lambda_j)]prod_i=1^nfracdlambda_isigmapi,;;lambda_iin[0,sigmapi],;;1leq ileq n,$$
$$S_N(x)=fracsin(Nx/2)sin(x/2),;;
L_N(x,y)=tfrac12sigma[S_rho N+tau(x-y)+varepsilon S_rho N+tau(x+y)].$$
The coefficients are tabulated as follows: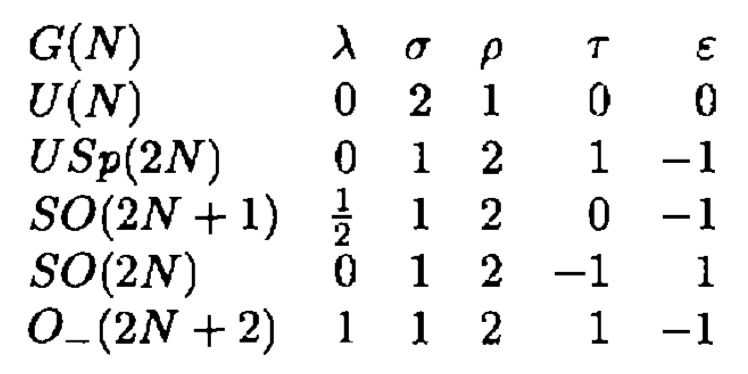
The group $rm SU,(N)$ is conspicuously missing from this table... I would assume there is a reason for this (Katz and Sarnak discuss $rm SU,(N)$ at various other points in their text). My surmise is that there is no way to incorporate the delta function $deltabigl(sum_i=1^N lambda_ibigr)$ into an $(N-1)times(N-1)$ determinant.
answered 1 hour ago
Carlo Beenakker
69k8155260
edited 1 hour ago
answered 1 hour ago
Carlo Beenakker
69k8155260
answered 1 hour ago
Carlo Beenakker
69k8155260
answered 1 hour ago
Carlo Beenakker
69k8155260
69k8155260
add a comment |Â
add a comment |Â
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f311314%2fintegral-kernel-function-for-the-sun-group%23new-answer', 'question_page');
);
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
