Characteristic impedance


This article is about impedance in electrical circuits. For impedance of electromagnetic waves, see Wave impedance. For characteristic acoustic impedance, see Acoustic impedance.



A transmission line drawn as two black wires. At a distance x into the line, there is current phasor I(x) traveling through each wire, and there is a voltage difference phasor V(x) between the wires (bottom voltage minus top voltage). If Z0displaystyle Z_0Z_0 is the characteristic impedance of the line, then V(x)/I(x)=Z0displaystyle V(x)/I(x)=Z_0V(x)/I(x)=Z_0 for a wave moving rightward, or V(x)/I(x)=−Z0displaystyle V(x)/I(x)=-Z_0V(x)/I(x)=-Z_0 for a wave moving leftward.




Schematic representation of a circuit where a source is coupled to a load with a transmission line having characteristic impedance Z0displaystyle Z_0Z_0.


The characteristic impedance or surge impedance (usually written Z0) of a uniform transmission line is the ratio of the amplitudes of voltage and current of a single wave propagating along the line; that is, a wave travelling in one direction in the absence of reflections in the other direction. Alternatively and equivalently it can be defined as the input impedance of a transmission line when its length is infinite. Characteristic impedance is determined by the geometry and materials of the transmission line and, for a uniform line, is not dependent on its length. The SI unit of characteristic impedance is the ohm.


The characteristic impedance of a lossless transmission line is purely real, with no reactive component. Energy supplied by a source at one end of such a line is transmitted through the line without being dissipated in the line itself. A transmission line of finite length (lossless or lossy) that is terminated at one end with an impedance equal to the characteristic impedance appears to the source like an infinitely long transmission line and produces no reflections.




Contents





  • 1 Transmission line model


  • 2 Derivation

    • 2.1 Using Telegrapher's Equation


    • 2.2 Using an Alternative Approach



  • 3 Lossless line


  • 4 Surge impedance loading


  • 5 Practical examples

    • 5.1 Coaxial cable



  • 6 See also


  • 7 References


  • 8 External links




Transmission line model




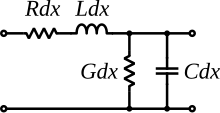
Schematic representation of an elemental length of a transmission line.


The characteristic impedance Z(ω)displaystyle Z(omega )displaystyle Z(omega ) of an infinite transmission line at a given angular frequency ωdisplaystyle omega omega is the ratio of the voltage and current of a pure sinusoidal wave of the same frequency travelling along the line. This definition extends to DC by letting ωdisplaystyle omega omega tend to 0, and subsists for finite transmission lines until the wave reaches the end of the line. In this case, there will be in general a reflected wave which travels back along the line in the opposite direction. When this wave reaches the source, it adds to the transmitted wave and the ratio of the voltage and current at the input to the line will no longer be the characteristic impedance. This new ratio is called the input impedance. The input impedance of an infinite line is equal to the characteristic impedance since the transmitted wave is never reflected back from the end. It can be shown that an equivalent definition is: the characteristic impedance of a line is that impedance which, when terminating an arbitrary length of line at its output, produces an input impedance of equal value. This is so because there is no reflection on a line terminated in its own characteristic impedance.


Applying the transmission line model based on the telegrapher's equations as derived below[1][2], the general expression for the characteristic impedance of a transmission line is:


Z0=R+jωLG+jωCdisplaystyle Z_0=sqrt frac R+jomega LG+jomega CZ_0=sqrt frac R+jomega LG+jomega C

where



Rdisplaystyle RR is the resistance per unit length, considering the two conductors to be in series,


Ldisplaystyle LL is the inductance per unit length,


Gdisplaystyle GG is the conductance of the dielectric per unit length,


Cdisplaystyle CC is the capacitance per unit length,


jdisplaystyle jj is the imaginary unit, and


ωdisplaystyle omega omega is the angular frequency.

Although an infinite line is assumed, since all quantities are per unit length, the characteristic impedance is independent of the length of the transmission line.


The voltage and current phasors on the line are related by the characteristic impedance as:


V+I+=Z0=−V−I−displaystyle frac V^+I^+=Z_0=-frac V^-I^-frac V^+I^+=Z_0=-frac V^-I^-

where the superscripts +displaystyle ++ and −displaystyle -- represent forward- and backward-traveling waves, respectively. A surge of energy on a finite transmission line will see an impedance of Z0 prior to any reflections arriving, hence surge impedance is an alternative name for characteristic impedance.



Derivation



Using Telegrapher's Equation




Consider one section of the transmission line for the derivation of the characteristic impedance. The voltage on the left would be V and on the right side would be V+dV. This figure is to be used for both the derivation methods.


The differential equations describing the dependence of the voltage and current on time and space are linear, so that a linear combination of solutions is again a solution. This means that we can consider solutions with a time dependence ejωt, and the time dependence will factor out, leaving an ordinary differential equation for the coefficients, which will be phasors depending on space only. Moreover, the parameters can be generalized to be frequency-dependent.[1]


Let


V(x,t)=V(x)ejωtdisplaystyle V(x,t)=V(x)e^jomega tdisplaystyle V(x,t)=V(x)e^jomega t and


I(x,t)=I(x)ejωtdisplaystyle I(x,t)=I(x)e^jomega tdisplaystyle I(x,t)=I(x)e^jomega t


The positive directions of V and I are in a loop of clockwise direction.


We find that


dV=−(R+jωL)Idx=−ZIdxdisplaystyle dV=-(R+jomega L)Idx=-ZIdxdisplaystyle dV=-(R+jomega L)Idx=-ZIdx


and


dI=−(G+jωC)Vdx=−YVdxdisplaystyle dI=-(G+jomega C)Vdx=-YVdxdisplaystyle dI=-(G+jomega C)Vdx=-YVdx


or


dVdx=−ZIdisplaystyle frac dVdx=-ZIdisplaystyle frac dVdx=-ZI


and


dIdx=−YVdisplaystyle frac dIdx=-YVdisplaystyle frac dIdx=-YV


These first-order equations are easily uncoupled by a second differentiation, with the results:


d2Vdz2−ZYV=0displaystyle frac d^2Vdz^2-ZYV=0displaystyle frac d^2Vdz^2-ZYV=0 and d2Idz2−ZYI=0displaystyle frac d^2Idz^2-ZYI=0displaystyle frac d^2Idz^2-ZYI=0


Both V and I satisfy the same equation. Since ZY is independent of z and t, it can be represented by a constant -k2. The minus sign is included so that k will appear as ±jkz in the exponential solutions of the equation. In fact,


V=V+e−γkz+V−eγkzdisplaystyle V=V^+e^-gamma kz+V^-e^gamma kzdisplaystyle V=V^+e^-gamma kz+V^-e^gamma kz


where V+ and V- are the constant of integration, The above equation will be the wave solution for V, and


I=(jk/Z)(V−e−γkz−V+eγkz)displaystyle I=(jk/Z)(V^-e^-gamma kz-V^+e^gamma kz)displaystyle I=(jk/Z)(V^-e^-gamma kz-V^+e^gamma kz)


from the first-order equation.[1]


If lumped  circuit analysis has to be valid at all frequencies, the length of the sub section must tend to Zero.[2]


limΔx→0ΔVΔx=dVdx=−(R+jωL)Idisplaystyle lim _Delta xto 0frac Delta VDelta x=frac dVdx=-(R+jomega L)Idisplaystyle lim _Delta xto 0frac Delta VDelta x=frac dVdx=-(R+jomega L)I


limΔx→0ΔIΔx=dIdx=−(G+jωC)Vdisplaystyle lim _Delta xto 0frac Delta IDelta x=frac dIdx=-(G+jomega C)Vdisplaystyle lim _Delta xto 0frac Delta IDelta x=frac dIdx=-(G+jomega C)V


Substituting the value of V in the above equation, we get.


ddxV+e−γx+V−e+γx=−(R+jωL)I+e−γx+I−e+γxdisplaystyle frac ddxV^+e^-gamma x+V^-e^+gamma x=-(R+jomega L)I^+e^-gamma x+I^-e^+gamma xdisplaystyle frac ddxV^+e^-gamma x+V^-e^+gamma x=-(R+jomega L)I^+e^-gamma x+I^-e^+gamma x


−γV+e−γx+γV−e+γx=−(R+jωL)I+e−γx+I−e+γxdisplaystyle -gamma V^+e^-gamma x+gamma V^-e^+gamma x=-(R+jomega L)I^+e^-gamma x+I^-e^+gamma xdisplaystyle -gamma V^+e^-gamma x+gamma V^-e^+gamma x=-(R+jomega L)I^+e^-gamma x+I^-e^+gamma x


Co-efficient of e−γxdisplaystyle e^-gamma xdisplaystyle e^-gamma x :  −γV+=−(R+jωL)I+displaystyle -gamma V^+=-(R+jomega L)I^+displaystyle -gamma V^+=-(R+jomega L)I^+


Co-efficient of eγxdisplaystyle e^gamma xdisplaystyle e^gamma x    :  γV−=−(R+jωL)I−displaystyle gamma V^-=-(R+jomega L)I^-displaystyle gamma V^-=-(R+jomega L)I^-


Since γ=(R+jωL)(G+jωC)displaystyle gamma =sqrt (R+jomega L)(G+jomega C)displaystyle gamma =sqrt (R+jomega L)(G+jomega C)


V+I+=R+jωLγ=R+jωLG+jωCdisplaystyle frac V^+I^+=frac R+jomega Lgamma =sqrt frac R+jomega LG+jomega Cdisplaystyle frac V^+I^+=frac R+jomega Lgamma =sqrt frac R+jomega LG+jomega C


V−I−=−R+jωLγ=R+jωLG+jωCdisplaystyle frac V^-I^-=-frac R+jomega Lgamma =sqrt frac R+jomega LG+jomega Cdisplaystyle frac V^-I^-=-frac R+jomega Lgamma =sqrt frac R+jomega LG+jomega C


It can be seen that, the above equations has the dimensions of Impedance (Ratio of Voltage to Current) and is a function of primary constants of the line and operating frequency. It is therefore called the “Characteristic Impedance” of the transmission line , often denoted by Zodisplaystyle Z_oZ_o.[2]


Zo=R+jωLG+jωCdisplaystyle Z_o=sqrt frac R+jomega LG+jomega Cdisplaystyle Z_o=sqrt frac R+jomega LG+jomega C


The formula of γdisplaystyle gamma gamma and Zodisplaystyle Z_oZ_o of a transmission line are very important. Many GATE memory based questions will be based on this formula. So remember  the equation and solve few questions related to the characteristic impedance of transmission line.[2]



Using an Alternative Approach


The line is modeled by a series of differential segments with differential series (Rdx, Ldx) and shunt(Cdx, Gdx) elements (as show on the figure above). The characteristic impedance is defined as the ratio of the input voltage to the input current of a semi-infinite length of line. We call this impedance Zo. That is, the impedance looking into the line on the left is Zo. But, of course, if we go down the line one differential length dx, the impedance into the line is still Zo. Hence we can say that the impedance looking into the line on the far left is equal to Zo in parallel with Cdx and Gdx, all of which is in series with Rdx and Ldx. That is:[3]


Zo=Rdx+jωLdx+Zo//(1/(Gdx+jωCdx)displaystyle Z_o=Rdx+jomega Ldx+Zo//(1/(Gdx+jomega Cdx)displaystyle Z_o=Rdx+jomega Ldx+Zo//(1/(Gdx+jomega Cdx)


where // means "in parallel with". Hence:


Zo=Rdx+jωLdx+1Gdx+jωCdx+1Zodisplaystyle Z_o=Rdx+jomega Ldx+frac 1Gdx+jomega Cdx+frac 1Z_odisplaystyle Z_o=Rdx+jomega Ldx+frac 1Gdx+jomega Cdx+frac 1Z_o


Zo=Rdx+jωLdx+ZoZo(Gdx+jωCdx)+1displaystyle Z_o=Rdx+jomega Ldx+frac Z_oZ_o(Gdx+jomega Cdx)+1displaystyle Z_o=Rdx+jomega Ldx+frac Z_oZ_o(Gdx+jomega Cdx)+1


Zo+Zo2(Gdx+jωCdx)=(Rdx+jωLdx)+Zo(Gdx+jωCdx)(Rdx+jωldx)+Zodisplaystyle Z_o+Z_o^2(Gdx+jomega Cdx)=(Rdx+jomega Ldx)+Z_o(Gdx+jomega Cdx)(Rdx+jomega ldx)+Z_odisplaystyle Z_o+Z_o^2(Gdx+jomega Cdx)=(Rdx+jomega Ldx)+Z_o(Gdx+jomega Cdx)(Rdx+jomega ldx)+Z_o


The product of two parentheses involves second order terms in dx, and hence these are discarded, leaving:


Zo=R+jωLG+jωCdisplaystyle Z_o=sqrt frac R+jomega LG+jomega Cdisplaystyle Z_o=sqrt frac R+jomega LG+jomega C[3]



Lossless line


The analysis of lossless lines provides an accurate approximation for real transmission lines that simplifies the mathematics considered in modeling transmission lines. A lossless line is defined as a transmission line that has no line resistance and no dielectric loss. This would imply that the conductors act like perfect conductors and the dielectric acts like a perfect dielectric. For a lossless line, R and G are both zero, so the equation for characteristic impedance derived above reduces to:


Z0=LC.displaystyle Z_0=sqrt frac LC.displaystyle Z_0=sqrt frac LC.

In particular, Z0displaystyle Z_0Z_0 does not depend any more upon the frequency.
The above expression is wholly real, since the imaginary term j has canceled out, implying that Z0 is purely resistive. For a lossless line terminated in Z0, there is no loss of current across the line, and so the voltage remains the same along the line. The lossless line model is a useful approximation for many practical cases, such as low-loss transmission lines and transmission lines with high frequency. For both of these cases, R and G are much smaller than ωL and ωC, respectively, and can thus be ignored.


The solutions to the long line transmission equations include incident and reflected portions of the voltage and current:



V=Vr+IrZc2εγx+Vr−IrZc2ε−γxdisplaystyle V=frac V_r+I_rZ_c2varepsilon ^gamma x+frac V_r-I_rZ_c2varepsilon ^-gamma x

displaystyle V=frac V_r+I_rZ_c2varepsilon ^gamma x+frac V_r-I_rZ_c2varepsilon ^-gamma x


I=Vr/Zc+Ir2εγx−Vr/Zc−Ir2ε−γxdisplaystyle I=frac V_r/Z_c+I_r2varepsilon ^gamma x-frac V_r/Z_c-I_r2varepsilon ^-gamma x

displaystyle I=frac V_r/Z_c+I_r2varepsilon ^gamma x-frac V_r/Z_c-I_r2varepsilon ^-gamma x
When the line is terminated with its characteristic impedance, the reflected portions of these equations are reduced to 0 and the solutions to the voltage and current along the transmission line are wholly incident. Without a reflection of the wave, the load that is being supplied by the line effectively blends into the line making it appear to be an infinite line. In a lossless line this implies that the voltage and current remain the same everywhere along the transmission line. Their magnitudes remain constant along the length of the line and are only rotated by a phase angle.


Surge impedance loading


In electric power transmission, the characteristic impedance of a transmission line is expressed in terms of the surge impedance loading (SIL), or natural loading, being the power loading at which reactive power is neither produced nor absorbed:


SIL=VLL2Z0displaystyle mathit SIL=frac V_mathrm LL ^2Z_0mathit SIL=frac V_mathrm LL ^2Z_0

in which VLLdisplaystyle V_mathrm LL V_mathrm LL is the line-to-line voltage in volts.


Loaded below its SIL, a line supplies reactive power to the system, tending to raise system voltages. Above it, the line absorbs reactive power, tending to depress the voltage. The Ferranti effect describes the voltage gain towards the remote end of a very lightly loaded (or open ended) transmission line. Underground cables normally have a very low characteristic impedance, resulting in an SIL that is typically in excess of the thermal limit of the cable. Hence a cable is almost always a source of reactive power.



Practical examples





























Standard
Impedance (Ω)
Tolerance

Ethernet Cat.5
100±5 Ω[4]

USB
90±15%[5]

HDMI
95±15%[6]

IEEE 1394
108
+3
−2%[7]

VGA
75±5%[8]

DisplayPort
100±20%[6]

DVI
95±15%[6]

PCIe
85±15%[6]


Coaxial cable


See also: Nominal impedance § 50 Ω and 75 Ω

The characteristic impedance of coaxial cables (coax) is commonly chosen to be 50 Ω for RF and microwave applications. Coax for video applications is usually 75 Ω for its lower loss.



See also


  • Ampère's circuital law

  • Characteristic acoustic impedance

  • Electrical impedance

  • Maxwell's equations

  • Transmission line

  • Wave impedance

  • Space cloth


References




  1. ^ abc "The Telegrapher's Equation". mysite.du.edu. Retrieved 2018-09-09..mw-parser-output cite.citationfont-style:inherit.mw-parser-output qquotes:"""""""'""'".mw-parser-output code.cs1-codecolor:inherit;background:inherit;border:inherit;padding:inherit.mw-parser-output .cs1-lock-free abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-lock-subscription abackground:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registrationcolor:#555.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration spanborder-bottom:1px dotted;cursor:help.mw-parser-output .cs1-hidden-errordisplay:none;font-size:100%.mw-parser-output .cs1-visible-errorfont-size:100%.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-formatfont-size:95%.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-leftpadding-left:0.2em.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-rightpadding-right:0.2em


  2. ^ abcd "Derivation of Characteristic Impedance of Transmission line". GATE ECE 2018. 2016-04-16. Retrieved 2018-09-09.


  3. ^ ab "Characteristic Impedance". www.ee.scu.edu. Retrieved 2018-09-09.


  4. ^ "SuperCat OUTDOOR CAT 5e U/UTP" (PDF). Archived from the original (PDF) on 2012-03-16.


  5. ^ "USB in a NutShell—Chapter 2—Hardware". Beyond Logic.org. Retrieved 2007-08-25.


  6. ^ abcd https://www.nxp.com/documents/application_note/AN10798.pdf (PDF) modified 2011-07-04


  7. ^ http://materias.fi.uba.ar/6644/info/reflectometria/avanzado/ieee1394-evalwith-tdr.pdf (PDF), modified 2005-06-11


  8. ^ http://www.promusic.cz/soubory/File/Downloads/Data%20sheet/Klotz/Kabely%20pro%20video/VMM5FL__e.pdf (PDF) modified 2009-12-07




  • Guile, A. E. (1977). Electrical Power Systems. ISBN 0-08-021729-X.


  • Pozar, D. M. (February 2004). Microwave Engineering (3rd ed.). ISBN 0-471-44878-8.


  • Ulaby, F. T. (2004). Fundamentals Of Applied Electromagnetics (media ed.). Prentice Hall. ISBN 0-13-185089-X.


External links


 This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".



  • IEEE: Differential Impedance... finally made simple (2000)







Comments

Post a Comment

Popular posts from this blog

What does second last employer means? [closed]

Image
Clash Royale CLAN TAG #URR8PPP .everyoneloves__top-leaderboard:empty,.everyoneloves__mid-leaderboard:empty margin-bottom:0; up vote -3 down vote favorite Say, for example I have worked in the following companies, Company A => 2010 - 2011 Company B => 2011 - 2012 Company C => 2012 - Till Date Company D => Have offer Now assume Company D is asking to submit documents from my second last employer. So from the list of companies given, which company would be qualified as second last employer? software-industry employer share | improve this question asked Aug 10 '14 at 5:16 Rajaprabhu Aravindasamy 559 1 6 13 closed as off-topic by Jim G., jmort253 ♦ Aug 11 '14 at 1:58 This question appears to be off-topic. The users who voted to close gave this specific reason: "Questions seeking advice on company-specific regulations, agreements, or policies should be directed to your manager or HR department. Questions that address...
Read more

List of Gilmore Girls characters

Image
The season three cast—(Back row): Lane, Michel, Paris, Emily, Richard, Sookie, Miss Patty, Kirk; Front row: Jess, Luke, Lorelai, Rory, Dean This is a list of characters for the comedy-drama television series Gilmore Girls . Contents 1 Main characters 1.1 Lorelai Gilmore 1.2 Rory Gilmore 1.3 Sookie St. James 1.4 Lane Kim 1.5 Michel Gerard 1.6 Luke Danes 1.7 Emily Gilmore 1.8 Richard Gilmore 1.9 Paris Geller 1.10 Dean Forester 1.11 Jess Mariano 1.12 Kirk Gleason 1.13 Jason Stiles 1.14 Logan Huntzberger 2 Major recurring characters 2.1 Christopher Hayden 2.2 Jackson Belleville 2.3 Mrs. Kim 2.4 Tristin DuGray 2.5 Max Medina 2.6 Taylor Doose 2.7 Dave Rygalski 2.8 Marty 3 Recurring characters 3.1 Stars Hollow 3.2 Chilton 3.3 Yale 3.4 Other 4 Notable guest stars 5 Unseen characters 6 Notes 7 References Main characters Actor Character Appearances Season 1 Season 2 Season 3 Season 4 Season 5 Season 6 Season 7 A Year in the Life Lauren Graham Lorelai Gilmore...
Read more

Confectionery

Image
Prepared foods made with a lot of sugar or other cabohydrates "Sweetmeat" redirects here. For the racehorse, see Sweetmeat (horse). Not to be confused with Sweetbread. This Kransekake is a traditional Scandinavian baker's confection. Confectionery is the art of making confections , which are food items that are rich in sugar and carbohydrates. Exact definitions are difficult. [1] In general, though, confectionery is divided into two broad and somewhat overlapping categories, bakers' confections and sugar confections. [2] Bakers' confectionery, also called flour confections , includes principally sweet pastries, cakes, and similar baked goods. Sugar confectionery includes candies ( sweets in British English), candied nuts, chocolates, chewing gum, bubble gum, pastillage, and other confections that are made primarily of sugar. In some cases, chocolate confections (confections made of chocolate) are treated as a separate category, as are sugar-free versions of ...
Read more